Algorithmique de
base de l'Infographie
Segments
Cercles
Ellipses
REMPLISSAGE
Polygone convexe
Polygone non convexe
Zones de pixels
de couleur
Algorithmes de tracé de segments
Algorithme de base pour beaucoup de traitements de l'Informatique Graphique:
- dessin en fil de fer,
- remplissage,
- élimination des parties cachées,
...
On désire tracer un segment entre deux points (xi,yi) et (xf,yf) de R2.
Ce tracé est effectué sur un écran bitmap (composé d'une matrice de n x m pixels carrés).
-> Le segment doit être discrétisé (rasterisé).


Problème: quels points tracer?
Trois impératifs:
Tout point du segment discret est traversé par le segment continu.
Tout point du segment discret touche au moins un autre point soit par l'un de ses cotés, soit par un de ses sommets (8-connexité).
On trace le moins de points possible.
On trace 1+max(abs(xi-xf),abs(yi-yf)) points.
Si abs(xi-xf) < abs(yi-yf), on trace un point et un seul par ligne interceptant le segment, sinon on trace un point et un seul par colonne interceptant le segment.

Bons tracés


Mauvais tracés
Tracé de segments par l'équation cartésienne
xf > xi, yf > yi et (xf-xi) >= (yf-yi)
-> Le coefficient directeur de la droite passant par les deux sommets est positif et inférieur ou égal à 1.
On utilise l’équation cartésienne de la droite:
y = a x + b avec a = ![]() et b = yi - a xi
et b = yi - a xi
void
ligne(int xi,int yi,
int xf,int yf) {
int x,y ;
double a,b ;
a =(double) (yf-yi)/(xf-xi) ;
b = yi - a * xi ;
for ( x = xi ; x <= xf ; x++ ) {
y = a * x + b ;
allume_pixel(x,y) ; }
}

Caractéristiques:
simplicité algorithmique
lenteur due à l'utilisation de réels, d'une division et de multiplications
Bresenham pour le tracé de segments
Algorithme incrémental en x et en y
Au cours de l'exécution, on quantifie pour chaque point la différence entre ses cordonnées entières (utilisées pour l’affichage) et réelles sur le segment continu.
xf > xi, yf >= yi, xf - xi > yf - yi
-> On allume un pixel en chaque abscisse entière x de xi à xf.
-> On utilise une variable cumul pour stocker la différence entre l'ordonnée entière et l'ordonnée réelle.
void ligne(int xi,int yi,int xf,int yf) {
int dx,dy,i,cumul,x,y ;
x = xi ;
y = yi ;
dx = xf - xi ;
dy = yf - yi ;
allume_pixel(x,y) ;
cumul = dx / 2 ;
for ( x = xi+1 ; x <= xf ; x++ ) {
cumul += dy ;
if (cumul >= dx) {
cumul -= dx ;
y += 1 ; }
allume_pixel(x,y) ; }
}
Le dernier point allumé a pour coordonnées (xf,yf) car dx/2+dy*dx est la valeur totale de ce qui a été ajouté à cumul.
![]() = dy.
= dy.
-> l’ordonnée du dernier point allumé est yi + dy = yf.
Caractéristiques
Plus grande complexité algorithmique apparente.
Rapidité due à l'utilisation exclusive d'entiers (valeurs maximales de l'ordre de la résolution de l'écran -> petites) et d'opérations arithmétiques simples sur ces entiers (additions, soustractions et comparaisons).
Algorithme adapté pour le tracé de tout segment
Utilisation de deux variables xinc et yinc pour gérer des incréments de 1 ou -1 pour x de xi à xf et y de yi à yf.

Deux parties dans l'algorithme:
une pour l'incrémentation en x,
l'autre pour l'incrémentation en y.
void ligne(int xi,int
yi,
int xf,int yf) {
int dx,dy,i,xinc,yinc,cumul,x,y ;
x = xi ;
y = yi ;
dx = xf - xi ;
dy = yf - yi ;
xinc = ( dx > 0 ) ? 1 : -1 ;
yinc = ( dy > 0 ) ? 1 : -1 ;
dx = abs(dx) ;
dy = abs(dy) ;
allume_pixel(x,y) ;
if ( dx > dy ) {
cumul = dx / 2 ;
for ( i = 1 ; i <= dx ; i++ ) {
x += xinc ;
cumul += dy ;
if (cumul >= dx) {
cumul -= dx ;
y += yinc ; }
allume_pixel(x,y) ; } }
else {
cumul = dy / 2 ;
for ( i = 1 ; i <= dy ; i++ ) {
y += yinc ;
cumul += dx ;
if ( cumul >= dy ) {
cumul -= dy ;
x += xinc ; }
allume_pixel(x,y) ; } }
}
Exemple d'exécution
Tracer le segment (3,2)-(18,11)
-> dx = 15, dy = 9.

x
y
cumul
3
2
7 (Dx/2)
4
2 -> 3
7+9 -> 16 -> 1
5
3
1+ 9 -> 10
6
3 -> 4
10 + 9 -> 19 -> 4
7
4
4 + 9 -> 13
8
4 -> 5
13 + 9 -> 22 -> 7
9
5 -> 6
7 + 9 -> 16 -> 1
10
6
1 + 9 ->10
11
6 -> 7
10 + 9 -> 19 -> 4
12
7
4 + 9 -> 13
13
7 -> 8
13 + 9 -> 22 -> 7
14
8 -> 9
7 + 9 -> 16 -> 1
15
9
1 + 9 ->10
16
9 -> 10
10 + 9 -> 19 -> 4
17
10
4 + 9 -> 13
18
10 -> 11
13 + 9 -> 22 -> 7



Bresenham pour le tracé de cercles
On désire tracer un arc de cercle de centre O et de rayon r circonscrit au second octant du plan.

-> On trace un arc entre les points
(0,r) et (![]() ,
,![]() ).
).
Un pixel sera allumé sur chaque
colonne d'abscisse comprise entre 0 et ![]() .
.
Si un pixel est allumé en position (x,y), le prochain pixel sera obligatoirement soit en position (x+1,y) soit en position(x+1,y-1) (tangente au cercle comprise entre 0 et -1 sur cette portion).

L'algorithme est basé sur l'étude, pour chaque colonne, de la position (vis à vis du cercle continu: au dessus ou en dessous) du point intermédiaire entre les deux pixels superposés définis ci-dessus qui encadrent le cercle (algorithme du midpoint).
Si ce point intermédiaire est situé dans le cercle (cas 1), le pixel allumé sera le pixel situé en dehors du cercle. Sinon, (cas 2), le pixel situé à l'intérieur du cercle est allumé.

L'idée de l'algorithme est donc de définir la position de chaque point intermédiaire de façon incrémentale, colonne après colonne.
La position d'un point P de coordonnées (x,y) vis à vis du cercle continu est donnée par l'équation cartésienne f(x,y) = x2 + y2 - r2.
-> Si f(x,y) < 0, P est dans le cercle, sinon il est à l'extérieur.
L'obtention d'un résultat négatif pour un point intermédiaire M conduit au choix du pixel extérieur E. Le prochain point intermédiaire sera situé en ME, c'est à dire un pixel à droite de M.

En revanche, un résultat positif conduit au choix du pixel intérieur SE, et au prochain point intermédiaire MSE situé un pixel à droite et un pixel plus bas que M.
P = (xp,yp) est la position d'un pixel allumé.
La variable dold calculée à partir de P est:
dold = f(xp+1,yp-![]() ) = (xp+1)2 + (yp-
) = (xp+1)2 + (yp-![]() )2 - r2.
)2 - r2.
(1) Si dold est inférieur à 0, E est choisi, le prochain point intermédiaire est ME, la valeur dnew est:
dnew = f(xp+2,yp-![]() ) = (xp+2)2 + (yp-
) = (xp+2)2 + (yp-![]() )2 - r2
)2 - r2
= dold + (2xp + 3).
(2) Si dold est supérieur à 0, SE est choisi, le prochain point intermédiaire est MSE, la valeur dnew est:
dnew = f(xp+2,yp-![]() ) = (xp+2)2 + (yp-
) = (xp+2)2 + (yp-![]() )2 - r2
)2 - r2
= dold + (2xp - 2yp + 5).
-> On obtient une définition récurrente incrémentale de d n'utilisant que des entiers.
La première valeur de d est obtenue
à partir de la position (0,r) pour un point intermédiaire de position placée en (1,r-![]() ).
).
-> dinit = 1 + r2 - r + ![]() - r2 =
- r2 = ![]() - r.
- r.
-> en entier: dinit = 1 - r.
On connaît maintenant totalement la définition récurrente de d.
-> on peut écrire une fonction où r est un paramètre entier placé en entête.
void
cercle(int r) {
int x,y,d ;
x = 0 ;
y = r ;
d = 1 - r ;
allume_pixel(x,y) ;
while ( y > x ) {
if ( d < 0 )
d += 2 * x + 3 ;
else {
d += 2 * (x - y) + 5 ;
y-- ; }
x++ ;
allume_pixel(x,y) ; }
}
Exemple d'exécution
Arc de cercle de 20 pixels de rayon: 15 pixels tracés

dold |
x |
y |
dnew |
0 |
20 |
-19 (1-r) |
|
-19 |
1 |
20 |
-19 + 2 *0 + 3 = -16 |
-16 |
2 |
20 |
-16 + 2 * 1 + 3 = -11 |
-11 |
3 |
20 |
-11 + 2 * 2 + 3 = -4 |
-4 |
4 |
20 |
-4 + 2 * 3 + 3 = 5 |
5 |
5 |
19 |
5 + 2 * (4 - 20) + 5 = -22 |
-22 |
6 |
19 |
-22 + 2 * 5 + 3 = -9 |
-9 |
7 |
19 |
-9 + 2 * 6 + 3 = 6 |
6 |
8 |
18 |
6 + 2 * (7 - 19) + 5 = -13 |
-13 |
9 |
18 |
-13 + 2 * 8 + 3 = 6 |
6 |
10 |
17 |
6 + 2 * (9 - 18) + 5 = -7 |
-7 |
11 |
17 |
-7 + 2 * 10 + 3 = 16 |
16 |
12 |
16 |
16 + 2 * (11 - 17) + 5 = 9 |
9 |
13 |
15 |
9 + 2 *(12 - 16) + 5 = 6 |
6 |
14 |
14 |
6 + 2 * (13 - 15) + 5 = 7 |



Le tracé d'ellipses
Un algorithme incrémental de tracé d'ellipses basé sur une technique du midpoint peut être défini. Le travail est compliqué par le fait que le tracé à l'intérieur d'un quadrant n'est plus symétrique par rapport à la diagonale.

L'algorithme réalisera le tracé en deux passes consécutives pour un quadrant. Par exemple pour le quadrant 1, une passe avec un pixel par colonne pour la région 1 et une passe avec un pixel par ligne pour la région 2. La limite entre ces deux régions est le point où la pente est de -1.
void
ellipse(long a,long b) {
int x,y ;
double d1,d2 ;
x = 0 ;
y = b ;
d1 = b*b - a*a*b + a*a/4 ;
allume_pixel(x,y) ;
while ( a*a*(y-.5) > b*b*(x+1) ) {
if ( d1 < 0 ) {
d1 += b*b*(2*x+3) ;
x++ ; }
else {
d1 += b*b*(2*x+3) + a*a*(-2*y+2) ;
x++ ;
y-- ; }
allume_pixel(x,y) ; }
d2 = b*b*(x+.5)*(x+.5) +
a*a*(y-1)*(y-1) - a*a*b*b ;
while ( y > 0 ) {
if ( d2 < 0 ) {
d2 += b*b*(2*x+2) + a*a*(-2*y+3) ;
y-- ;
x++ ; }
else {
d2 += a*a*(-2*y+3) ;
y-- ; }
allume_pixel(x,y) ; }
}
Définition
Clipping: Tout traitement permettant de réduire le dessin d'un objet graphique à une région de l'écran.
Cette région est classiquement un rectangle mais peut être de toute autre forme.
Autre traitement de base de l'Informatique Graphique.
Exemple: clipping de 2 segments à l'intérieur d’un rectangle.

Cohen-Sutherland pour le clipping à l’intérieur d’un rectangle
Algorithme basé sur une technique de détection d’un certain nombre de cas de figure de position d'un segment vis à vis d'un rectangle.
On associe à chaque extrémité du segment un code sur quatre valeurs booléennes indiquant la position (x,y) du sommet par rapport aux quatre droites définissant le rectangle de clipping (xmin, xmax)-(ymin, ymax):
la première valeur = 1 si x < xmin,
la deuxième valeur = 1 si x > xmax,
la troisième valeur = 1 si y < ymin,
la quatrième valeur = 1 si y > ymax.

Dans trois cas on sait si un segment de coordonnées (xi,yi)-(xf,yf) passe ou ne passe pas à l’intérieur du rectangle (xmin,ymin)-(xmax,ymax):
Si les codes des deux extrémités sont entièrement égaux à zéro (cas (1)), le segment est entièrement dans le rectangle de clipping.
Si un seul des codes des deux extrémités est entièrement égal à zéro, le segment est pour partie dans le rectangle de clipping (cas (2)).
Si aucun des codes des extrémités n'est entièrement égal à zéro, on calcule le "et logique" entre les deux codes. Si un 1 apparaît en position 1, 2, 3 ou 4, le segment est obligatoirement situé à l’extérieur du rectangle (cas (3)). Dans l'autre cas, on ne peut pas conclure avec certitude (cas (4)).

Principe
A partir du segment s initial, ramener progressivement ses deux extrémités sur les droites AB, BD, AC ou CD jusqu'à établir que s n'appartient pas à ABDC ou bien que les codes des deux extrémités sont uniformément égaux à 0.
Au cours de l'exécution, chaque fois qu’il est établi qu'une des valeurs du code d'une extrémité n'est pas égale à zéro, on ramène cette valeur à zéro en déplaçant l'extrémité pour qu'elle vienne rejoindre l'une des droites AB, BD, AC ou CD.

Cet algorithme de clipping peut facilement être adapté à R3 pour le clipping de segments de droites à l’intérieur d’un parallélépipède rectangle.
Algorithme
procedure
clip(point_2D p1,
point_2D p2,
fenetre f) {
code c1,c2 ;
point_2D p ;
c1 = code(p1,f) ;
c2 = code(p2,f) ;
tant que (c1 ou c2 contient un 1) et
(c1 et c2 n'ont pas de 1
en commun) {
si c1 uniformément 0 {
inverser p1 et p2 ;
c1 = c2 ; }
si code 0 de c1 = 1 {
abscisse de p1 = abscisse
intersection entre (P1,P2)
et horizontale en ymax de f ;
ordonnée de p1 = ymax de f ; }
sinon
si code 1 de c1 = 1 {
abscisse de p1 = abscisse
intersection entre (P1,P2)
et horizontale en ymin de f ;
ordonnée de p1 = ymin de f ; }
sinon
si code 2 de c1 = 1 {
ordonnée de p1 = ordonnée
intersection entre (P1,P2)
et verticale en xmax de f ;
abscisse de p1 = xmax de f ; }
sinon
si code 3 de c1 = 1 {
ordonnée de p1 = ordonnée
intersection entre (P1,P2)
et verticale en xmin de f ;
abscisse de p1 = xmin de f ; }
c1 = code(p1,f) ;
c2 = code(p2,f) ; }
si c1 et c2 ne contiennent pas de 1
tracer entre p1 et p2 ;
}


Définition
Ligne brisée: toute suite non circulaire de points reliés par des segments.
Polygone: toute suite circulaire de points reliés par des segments.


Remplissage d’un polygone convexe
Remplissage trame après trame en commençant du sommet inférieur et en remontant les trames tout en gérant le parcours des suites de faces droites et gauches.

Suite gauche: B, A, F, E
Suite droite: B, C, D, E
Remplissage d’un polygone éventuellement concave

Principe
Processus de remplissage traçant les trames internes au polygone les unes à la suite des autres.
Chaque trame interceptera un nombre paire n de cotés du polygone.
Après tri en x des n intersections Pi (1 <= i <= n), on tracera des
segments entre chaque couple de coordonnées (P2*j-1,P2*j) avec 1
<= j <= ![]() .
.

Mise en œuvre
Une liste chaînée LCA permet de gérer une suite de cotés actifs.
Cette liste indiquera quels sont les cotés ayant une intersection avec la trame en cours de traitement.
Elle est mise à jour à chaque avancée d’une trame au cours de l’exécution de l’algorithme.
Elle est triée en permanence par ordre croissant des abscisses x des points intersections.

LCA pour la trame 7

LCA pour la trame 13
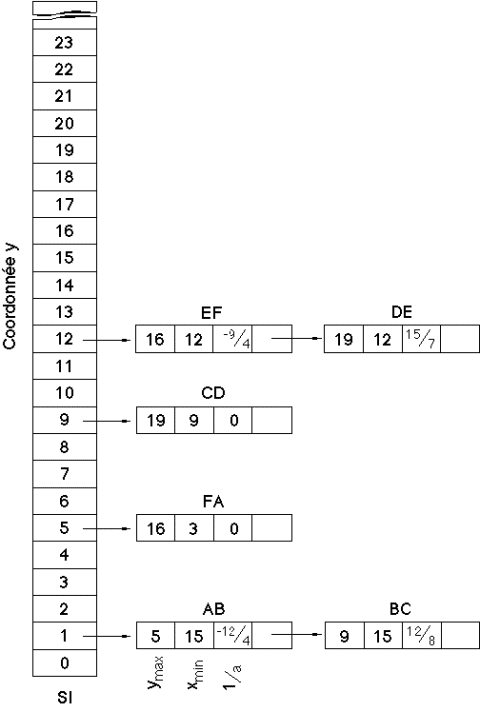
Création d’une structure intermédiaire SI contenant les informations qui seront nécessaires à la gestion de LCA.
SI est un tableau de listes chaînées.
Pour chaque coordonnée y, on stocke l’ensemble des cotés c du polygone tels que y est l'ordonnée minimale ymin des deux extrémités de c.
(1) En parcourant SI on pourra savoir quels cotés devront entrer dans LCA pour telle ou telle ordonnée.
(2) Pour gérer le retrait des cotés de LCA, on mémorise l'ordonnée maximale de chaque coté.
On stocke aussi pour chaque coté:
- l’inverse 1/a de son coefficient directeur (incrément en x pour un déplacement unitaire en y),
- l’abscisse xmin correspondant à ymin.
Les listes de SI sont triées par ordre croissant de xmin, puis pour deux xmin identiques, par ordre croissant de la valeur 1/a. Ce tri a pour but de faciliter le déplacement des cotés vers LCA car cet ordre de classement devra être respecté dans LCA.

Algorithme
Procedure remplir_polygone(p:polygone) ;
début
créer la structure SI
initialiser la structure LCA à vide
pour chaque trame intersectant le polygone
début
gérer les entrées dans LCA à partir
de SI
gérer les sorties de LCA à partir
des informations contenues dans SI
afficher tous les morceaux de trames
décrits dans LCA
fin
fin
Remplissage d'une zone définie par une couleur
Définition
On entend par zone définie par une couleur:
(1) un ensemble connexe maximum de pixels de couleurs identiques,
(2) un ensemble connexe maximum de pixels dont la couleur n'est pas une couleur définie.

cas (1) : chacune des zones grise et noire.
cas (2) : l'union des zones grise et noire vis à vis de la zone blanche.
Le remplissage est réalisé à partir d'un pixel germe.
Un premier algorithme
Principe
Au cours du remplissage, à chaque fois qu'un pixel devant être rempli est touché, on le remplit, puis on relance récursivement l'algorithme sur les pixels qui lui sont connexes.
Algorithme
L'implantation est naturellement récursive.
void remplissage(int x,int y,
int c,int cl) {
cp = getpixel(x,y) ;
if ( ( cp != cl ) && ( cp != c ) ) {
putpixel(x,y,c) ;
remplissage(x,y+1,c,cl) ;
remplissage(x,y-1,c,cl) ;
remplissage(x+1,y,c,cl) ;
remplissage(x-1,y,c,cl) ; }
}
L'utilisation de la récursivité entraîne très fréquement des problèmes de dépassement de capacité de la pile si les zones remplies sont trop grandes.
Un deuxième algorithme
Principe
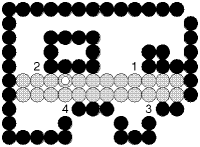
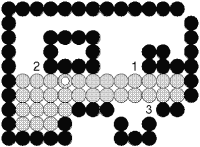
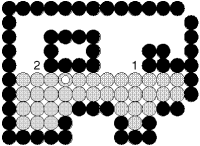
Le remplissage est effectué suite horizontale maximale de pixels après suite horizontale à partir d'un pixel germe initial.
A chaque itération:
On remplit tous les pixels pi jusqu'à la couleur limite à droite et à gauche du germe courant.
On recherche parmi les pixels au dessus et en dessous des Pi ceux qui sont le plus à droite d'une suite horizontale maximale à remplir.
Ces pixels sont empilés comme germes des itérations suivantes.



...
Algorithme
L'implantation nécessite la définition d'une pile de positions de germes. L'algorithme prend la forme d'une boucle exécutée tant que la pile n'est pas vide.
void remplissage(int xx,int yy,
int c,int lim) {
int x,y,xi,xf ;
p.sp = 1 ;
p.x = calloc(1000,sizeof(int)) ;
p.y = calloc(1000,sizeof(int)) ;
p.x[0] = xx ;
p.y[0] = yy ;
setcolor(c) ;
while ( p.sp != 0 ) {
xi = xf = x = p.x[p.sp-1] ;
y = p.y[p.sp-1] ;
x++ ;
cp = getpixel(x,y) ;
while ( cp != lim ) {
xf = x ;
x++ ;
cp = getpixel(x,y) ; }
x = p.x[p.sp-1]-1 ;
cp = getpixel(x,y) ;
while ( cp != lim ) {
xi = x ;
x-- ;
cp = getpixel(x,y) ; }
line(xi,y,xf,y) ;
p.sp-- ;
x = xf ;
while ( x >= xi ) {
cp = getpixel(x,y+1) ;
while ( ((cp == lim) || (cp == c))
&&
(x >= xi) ){
x-- ;
cp = getpixel(x,y+1) ; }
if ( (x >= xi) && (cp != lim)
&& (cp != c) ) {
p.x[p.sp] = x ;
p.y[p.sp] = y+1 ;
p.sp++ ; }
cp = getpixel(x,y+1) ;
while ( ( cp != lim )
&&
( x >= xi ) ) {
x-- ;
cp = getpixel(x,y+1) ; } }
x = xf ;
while ( x >= xi ) {
cp = getpixel(x,y-1) ;
while ( ((cp == lim) || (cp == c))
&&
(x >= xi) ){
x-- ;
cp = getpixel(x,y-1) ; }
if ( (x >= xi)
&& (cp != lim)
&& (cp != c) ) {
p.x[p.sp] = x ;
p.y[p.sp] = y-1 ;
p.sp++ ; }
cp = getpixel(x,y-1) ;
while ( ( cp != lim )
&&
( x >= xi ) ) {
x-- ;
cp = getpixel(x,y-1) ; } } }
free(p.x) ;
free(p.y) ;
}
