Le placage
de texture
Placage (ou plaquage, ou mappage) de texture : Technique visant à dessiner un objet de manière à ce que les surfaces apparaissant sur cet objet soient revêtues d’une image.
Problème : Attribuer une teinte à tout pixel appartenant à un objet en fonction :
d’une ou de plusieurs sources lumineuses,
d’une orientation de l’objet en ce pixel :
-> diffusion Lambertienne,
des coordonnées réelles du point de l’objet correspondant au pixel de l’image :
-> calcul d’une teinte fonction de la teinte dans la texture plaquée.
Méthodologie
On dispose d’une surface paramétrique sur laquelle on désire plaquer une texture.
Problème: Associer à chaque pixel de l’image une couleur puisée dans l’image à plaquer.
Simplification: On considère le placage d’une image sur une seule facette.
Problème : définir un changement de repère M(xfac,yfac,zfac) -> (xima,yima), permettant d’associer à chaque point de la facette, un point à l’intérieur de l’image à plaquer.

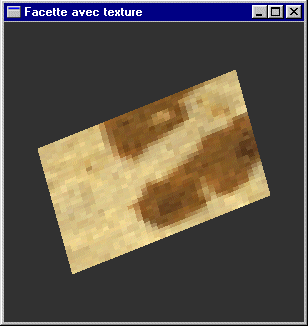
Exemple

Image placée

Résultat
Problème
Placer la même texture sur plusieurs facettes jointives:
-> des difficultés pour obtenir la continuité de la texture quand on passe d’une facette à une autre.
Adapter le changement de repère pour recoller les facettes (Aima,Bima,Cima) les unes à coté des autres en fonctions des positions des facettes (Afac,Bfac,Cfac) dans la scène.
Admettre des déformations de la texture. Il est alors préférable de gérer des facettes quadrangulaires plutôt que des facettes triangulaires.

Une même classe de problèmes se pose pour les objets paramétriques. L'utilisation des équations paramétriques fournit une solution au problème des discontinuités, mais produit des écrasements et des distensions tels que l'origine 2D de la texture est clairement visible.
Exemple

Image placée

Résultat après placage sur une sphère


L’image source est une bitmap.
Chaque point p = (xima,yima) correspondant à un pixel pf = (xfac,yfac,zfac) de la facette sera naturellement associé à un pixel (xb,yb) d'une bitmap.
Intérêt:
Simplicité.
placage de textures scannées.
Inconvénient:
Le stockage d'une image peut demander beaucoup de mémoire.
Si l'observateur est placé trop près de la facette mappée, on visualise les pixels de l'image source.
Exemple

Image placée

Résultat après placage sur une sphère
Texture mathématique ou paramétrique
Utilisation d’une fonction Couleur(x,y) pour définir l’image source.
Chaque point p = (x,y) correspondant à un pixel pf = (xfac,yfac,zfac) de la facette permettra de calculer la couleur Couleur(x,y) du pixel pf.
Les textures mathématiques sont fréquemment utilisées pour représenter des surfaces naturelles non régulières. Elles sont alors basées sur des fractales ou des fonctions de bruit Brownien fractionnaire approximmées par des techniques à base de subdivision récursive. C'est par exemple le cas des textures à base de bruit de Perlin (Perlin Noise).
Intérêt :
Les textures mathématiques permettent des zooms sur les objets sans avoir d’effet de pixélisation si on se rapproche à une distance telle qu’un pixel de l’image source correspond à plus d’un pixel à l’écran.
Le codage d'une fonction mathématique est économique en mémoire.
Inconvénient:
Toute image n’est pas stockable sous la forme d’une texture mathématique.
Cette solution est peu économique en CPU.
Exemples

Veinures sur du bois
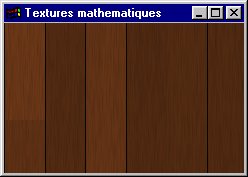
Lattes de parquet

Granite

Marbre
Problème: Les textures définies précédemment peuvent laisser apparaître leurs origines 2D.
Exemple: Le placage d’une texture représentant du bois sur une sphère, un cône, un cube,… montrera que la texture est peinte car elle ne fera pas apparaître correctement les veinures.

Solution: Utiliser une texture solide c’est à dire une texture mathématique dans laquelle la fonction couleur n’est plus une fonction de R2 mais une fonction de R3.
A chaque point p = (x,y,z) de l’espace global correspondant à un pixel affiché (xfac,yfac,zfac) sur une facette à l’écran correspondra directement une couleur Couleur(x,y,z).
La définition d’une texture solide est toujours mathématique, car le stockage d’un espace voxel demande trop de mémoire.
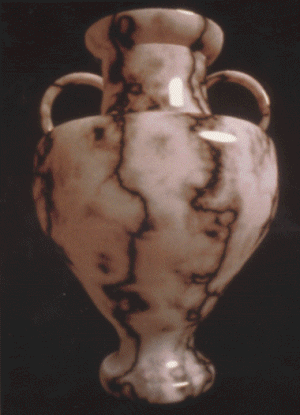
Un vase

Un cube érodé

Une sphère érodée
Modulation de la normale : Bump Mapping
La technique de Bump Mapping est basée sur une modulation de la normale (utilisée pour les calculs d’éclairement) permettant de faire apparaître des fluctuations d'éclairage sur des surfaces planes.
On peut ainsi donner l'illusion d'un relief.
Exemple

Image utilisée comme Bump

Résultat après placage sur des sphères
Le placage de texture est très largement utilisé en synthèse d'images pour améliorer la qualité des vues obtenues.
Le bump-mapping correspond plutôt à un soucis de simplification des scène par diminution du nombre de facettes.
Ces deux techniques sont assez gourmandes en temps de calcul et/ou en mémoire.
