Le rendu par lancer
de rayons
(ray tracing)
Effectuer en sens inverse de la réalité le parcours des rayons lumineux. Ainsi, on traverse l'écran depuis l'œil de l'observateur de manière à déterminer de quels objets les rayons proviennent, et ainsi, à déterminer leurs caractéristiques chromatiques.
On traite le rayon passant par l’observateur et chaque pixel de l'écran de manière à déterminer si ce rayon intercepte un objet de la scène.
Deux cas sont alors possibles:
(1) Aucun objet n'intercepte le rayon
-> La couleur est celle du fond.
(2) Des objets interceptent le rayon
-> On trouve l'objet le plus proche de l'observateur.
-> En fonction des caractéristiques de cet objet vis à vis de la lumière, la teinte du pixel est calculée à partir des composantes de lumière (a) diffusée, (b) réfléchie et (c) transmise par l'objet au point d'intersection.
Le programme
(a) Valeur diffusée:
On devra:
- déterminer le point d'intersection P entre l'objet et le rayon incident,
- lancer un rayon de ce point vers chacune des sources lumineuses présente dans la scène pour déterminer si ce rayon est intercepté ou non,
- pour chaque rayon non intercepté, appliquer une formule adaptée au calcul de la lumière diffuse (loi de Lambert ou autre)
- sommer le résultat de chacun de ces calculs pour obtenir la lumière diffusée.
(b) La valeur obtenue par réflexion est calculée en relançant récursivement l'algorithme de lancer de rayons à partir du point d’intersection P selon la direction de réflexion du rayon initial puis en multipliant la valeur obtenue par le coefficient de réflexion de la surface de l'objet.
La direction de réflexion qr est telle que qr = -qi où qi est "l'angle d'incidence" par rapport à la normale à l'interface au niveau du point de réflexion.
Angle de réflexion
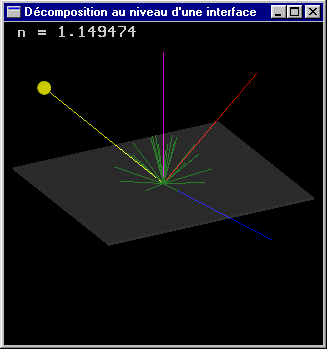
(c) La valeur obtenue par transmission est calculée en relançant récursivement l'algorithme de lancer de rayons à partir du point d'intersection P selon la direction de transmission puis en multipliant cette valeur par le coefficient de transmission de la surface de l'objet.
La direction du rayon incident est modifiée selon la loi de Snell:
ni sin qi = nt sin qt
où ni est l’indice de réfraction du matériau dans lequel se propage le rayon incident, nt est l’indice du matériau dans lequel se propage le rayon transmis, qi est "l'angle d'incidence" par rapport à la normale à l'interface au niveau du point de transmission et qt est "l'angle de transmission" par rapport à cette même normale.
Angle de transmission
En fonction de ni, nt et qi, la valeur de qt peut ne pas être définie (cas où le rayon incident fait un angle avec la normale suffisant pour ne pas être transmis et être totalement réfléchi (effet miroir)).
Algorithme simplifié
Programme lancer_de_rayonsmémoriser une scène s
pour chaque pixel p(x,y) de l'écran
calculer les composantes géométriques
du rayon r passant par l'observateur
et p
teinte de p(x,y) <- lancer_rayon(s,r)
finpour
finprog
couleur lancer_rayon(scene s,rayon r)
couleur cr,ct,cd
rayon rr,rt,rd
point p
début
déterminer l'objet o de la scène s dont
l'intersection avec r est la plus proche
de la source de r
si o n'existe pas
lancer_rayon <- noir
sinon
calculer le point d'intersection p
rr <- rayon réfléchi de r en p
vis à vis de o
rt <- rayon transmis de r en p
vis à vis de o
cr <- lancer_rayon(s,rr)
ct <- lancer_rayon(s,rt)
cd <- noir
pour chaque source lumineuse sl de s
calculer le rayon rd de p vers sl
si rd non intercepté par un objet
cd <- cd +
lumière_diffuse(sl,o,rd)
finsi
finpour
lancer_rayon <- cr + cd + ct
finsi
fin_fonction
Avantages du lancer de rayons
Réalisme
Des effets tels que les réflexions et les transparences sont restitués. Aucun autre algorithme n'est capable de modéliser ces effets de manière aussi satisfaisante.
Les parties cachées sont éliminées
de manière intrinsèque. Au niveau 1 de la récursivité on est en présence d’un
Z-Buffer (Ray Casting).
Les ombres portées sont elles aussi intrinsèques au modèle.
Objets de base évolués
Pas de décomposition de la scène en
facettes ou surfaces élémentaires
-> les objets lisses apparaissent réellement lisses.
Les opérations de base utilisées sont les tests d'intersection objet<->rayon. Ces tests sont implantés au moyen des équations paramétriques par résolution de systèmes d’équations.
Classiquement les objets modélisant une scène affichée en lancer de rayon sont des sphères, des parallélépipèdes rectangles, des cônes,… (affectés de rotations, translations, zooms, affinités).
Inconvénients du lancer de rayons
Récursivité
A chaque interception d'un objet par un rayon, on lance deux rayons: un rayon pour les transparences et un rayon pour les réflexions.
-> une explosion exponentielle probable du nombre total de rayons tracés à l'intérieur de la scène car si n est le niveau de profondeur de la récursivité, il y a de l'ordre de 2n rayons tracés pour chaque pixel.
Pour obtenir un certain réalisme le niveau de récursivité doit être poussé assez loin (au moins 8) et donc les temps de calcul sont très longs (plusieurs heures pour des scènes complexes).
Problèmes de calcul d'illumination
Le lancer de rayons ne peut pas restituer un effet tel que la propagation de la lumière à l'intérieur d'une loupe (obtention d’une concentration ou d’une atténuation lumineuse en certaines zones).
On ne peut pas restituer la diffusion de la lumière dans les matériaux (en particulier l’air)
-> le non réalisme de certaines ombres.
L’illumination est "moyennement" locale c’est à dire qu’elle provient toujours quasiment directement d’une source de lumière répertoriée comme telle, tandis que dans la réalité toutes les surfaces et tous les milieux sont récepteurs et émetteurs de lumière
-> lumières très crues et zones non éclairées.
Ce problème est partiellement résolu en attribuant une composante de lumière ambiante à chacun des éléments de la scène (composante souvent constante car on ne sait pas la calculer précisément, ajoutée aux autres).
Des ombres portées
Des réflexions
Des transmissions à travers des billes d'indices de réfraction 1.333, 1.5, 2.5 et 4 (de gauche à droite et de bas en haut).
Noter l'inversion des objets.
Quelques problèmes mathématiques
Calcul du rayon réfléchi
Soient:
le vecteur normé
inverse à la direction d’incidence de la source lumineuse,
le vecteur normé
réfléchi,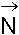
la normale à
l’interface orientée dans la matériau où se propage le rayon incident.
Calcul du rayon transmis
Soient:
- le vecteur normé inverse à la
direction d’incidence de la source lumineuse,
le vecteur normé transmis,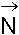- la normale à l’interface
orientée dans le matériau où se propage le rayon incident
le vecteur normé
perpendiculaire à 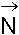situé dans le plan déterminé par et .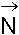
Si on pose n = 
, on obtient:
Ce qui nous conduit pour finir à:
qui ne contient que des quantités connues.
Calculs d'intersection
Intersection entre une sphère et un rayon
On désire connaître la position de(s) intersection(s) entre un rayon lumineux quelconque et une sphère de rayon r centrée sur l'origine.
Par substitution on obtient:
(a1t + b1)2+(a2t + b2)2+(a3t + b3)2 = r2
(a12+a22+a32)t2 + 2(a1b1+a2b2+a3b3)t + b12+b22+b32 = r2
équation du second degré en t impliquant 0, 1 ou 2 intersections en fonction des conditions initiales.
Intersection entre une facette triangulaire et un rayon
On désire connaître la position de l'intersection (si elle existe) entre un rayon et une facette triangulaire connue par les coordonnées dans l’espace de ses trois sommets A, B et C.
On a donc: A = 
, B = 
et C = 
.
B-A =
, C-A =
.
Le système à résoudre est 
-> 
.
On doit résoudre ce système de trois équations linéaires à trois inconnus
La solution est:
D = - z1 y3 x2 + y1 z3 x2 + x3 z1 y2 + y3 x1 z2 - z3 x1 y2 - x3 y1 z2
u = - (- y3 x2 zA - y3 xP z2 + y3 x2 zP + y3 xA z2 + x3 y2 zA - x3 y2 zP + x2 z3 yA - x2 z3 yP + xP z3 y2 + x3 yP z2 - x3 yA z2 - xA z3 y2)/D
v = (- x3 z1 yA - x3 y1 zP + x3 z1 yP + x3 y1 zA + z3 x1 yA + y1 z3 xP + z1 y3 xA - z3 x1 yP - y3 x1 zA - y1 z3 xA + y3 x1 zP - z1 y3 xP)/D
t = (- xP z1 y2 + xP y1 z2 + xA z1 y2 - xA y1 z2 - x1 y2 zA + x1 y2 zP - x1 yP z2 + x1 yA z2 - x2 z1 yA - x2 y1 zP + x2 z1 yP + x2 y1 zA)/D
Pour que le point d’intersection soit à l’intérieur du triangle ABC, il faut que:
D soit différent de zéro (sinon le rayon est parallèle au plan),
u soit positif,
v soit positif,
u+v soit inférieur ou égal à 1.
Si on pose dx = xP - xA, dy = yP - yA, dz = zP - zA
D = z1y3x2-y1z3x2-x3z1y2-y3x1z2+z3x1y2+x3y1z2
v = -
u = 
t = -
Les optimisations classiques mises en œuvre autour de l'algorithme du lancer de rayons portent sur l'amélioration de trois facteurs clés:
le calcul des intersections -> amélioration des tests d'intersection,
le nombre de calculs d'intersection -> diminution de ce nombre,
le nombre de rayons tracés -> diminution du nombre de rayons primaires, diminution du nombre rayons secondaires.
Le calcul des intersections
Le test d'intersection est l'opération de base de tout algorithme de lancer de rayon. Son optimisation pour les différents objets pris en compte permet des gains de temps substantiels.
Représentation mémoire des objets
Tout objet sera représenté sous la forme d'un objet canonique auquel on applique une matrice de transformation M en coordonnées homogènes (exemple: le cube de centre O et de rayon 1.0 pour tous les parallélépipèdes rectangles).
Test d'intersection avec un rayon R:
Appliquer à R la matrice M-1 pour obtenir le rayon R',
Déterminer l'intersection entre R' et l'objet canonique,
S'il y a une intersection, calculer sa position et les rayons réfléchi et transmis
Appliquer la matrice M pour fixer définitivement ces rayons dans l'espace.
Boites englobantes
La réalisation d'un test d'intersection pour un objet canonique peut entraîner une charge de calcul importante (tore par exemple).
En englobant strictement chaque objet dans une "boite" géométrique simple (test d'intersection simple), définie en coordonnées globales, on pourra réaliser une économie substantielle car un rayon qui ne touche pas la boite ne pourra pas toucher l'objet.
Le nombre de calculs d'intersections
L'acquisition de connaissances sur la position des objets à l'intérieur de la scène peut éviter la réalisation obligatoire d'une recherche systématique d'intersection.
Décomposition en voxels
Une technique classique consiste à décomposer l'espace en voxels et à associer à chaque voxel v la liste des objets partiellement ou totalement inclus dans v.
Plutôt que de parcourir séquentiellement tous les objets de la scène, on analyse les listes d'objets des voxels, voxel après voxel depuis le voxel d'émission du rayon.
Sitôt qu'une intersection est trouvée, il n'est plus nécessaire de parcourir d'autres voxels car tout autre intersection est plus éloignée du point d'émission.
Le nombre de rayons tracés
Une solution simple pour diminuer le nombre de rayons primaires consiste à effectuer préalablement au lancer de rayon une projection des objets de la scène sur l'écran de visualisation. On saura ainsi quels sont les pixels en lesquels aucun objet n'apparaît.
Les problème de la diminution du nombre de rayons secondaires est complexe et ne sera pas traité ici.
Le lancer de rayons est correct du point de vue géométrique pour le placement des rayons lumineux à l'intérieur d'une scène.
Il est en revanche beaucoup moins correct du point de vue énergétique car les phénomènes que l’on désire rendre sont des transports d’énergie, choses que le lancer de rayons ne traduit que partiellement. Ils sont beaucoup plus compliqués que ceux que l’on peut modéliser par des simples calculs géométriques.
Un avantage déterminant du lancer de rayons pour l'obtention d'images photoréalistes est toutefois que cet algorithme permet de rendre les réflexions et les transparences.
Par rapport à un algorithme du Z-Buffer + Gouraud ou Phong, les images sont de bien meilleure qualité, mais les temps de calcul sont généralement considérablement plus longs (multipliés par 100, 1000 ou plus).